Binary Search Tree는 진짜 중요한 개념이다.
Binary Tree를 저번 시간에 배웠고 이 Binary Tree를 다시 상기해보면 자식이 최대 2개까지만 있는 노드로만 구성되어 있는 트리를 Binary Tree라고 했고 이 트리를 탐색하는 방법 중 대표적인 두 가지 DFS, BFS가 있다고 했다.
DFS(Depth First Search)는 깊이 우선 탐색으로 밑으로 더 내려갈 수 없을때까지 계속 아래로 찾아나가는 방식.
BFS(Breadth First Search)는 한 노드의 모든 라인을 다 검색하고 그 바로 다음 아래 라인을 다 검색해가면서 찾아내는 방식이라고 했다.
Binary Search Tree
Binary Search Tree는 Binary Tree에 특정한 룰을 추가한 트리구조이다.
어떤 룰일까? 한 노드를 기준으로 왼쪽 Sub tree는 지금 노드보다 무조건 더 작은값, 오른쪽 Sub tree는 지금 노드보다 무조건 더 큰 값으로만 구성되어 있는 구조를 Binary Search Tree라고 한다.

이 트리는 완벽한 Binary Search Tree이다. 모든 노드를 기준으로 비교해도 왼쪽 Sub tree는 본인보다 작은 값을 가지고 있고, 오른쪽 Sub tree는 본인보다 큰 값을 가지고 있기 때문.
이 구조가 왜 좋고 왜 자주 사용될까? 절반 소거법(Binary Search), 다른말로 '분할 정복 방식'이 가능하기 때문에 효율적으로 원하는 값을 찾아낼 수 있기 때문이다.
예를 들어 저 트리에서 10을 찾고 싶다고 해보자. 다음 단계를 거쳐간다.
1단계

처음 루트 노드에게 10이거나 10보다 크니? 라고 물어봐서 10이면 끝. 10이 아닌 경우 10보다 작다고 말할 테니 오른쪽으로 이동.
여기서 오른쪽으로 이동하면 5를 기준으로 왼쪽은 볼 필요가 없어진다. 이게 절반 소거법의 장점이다.
2단계
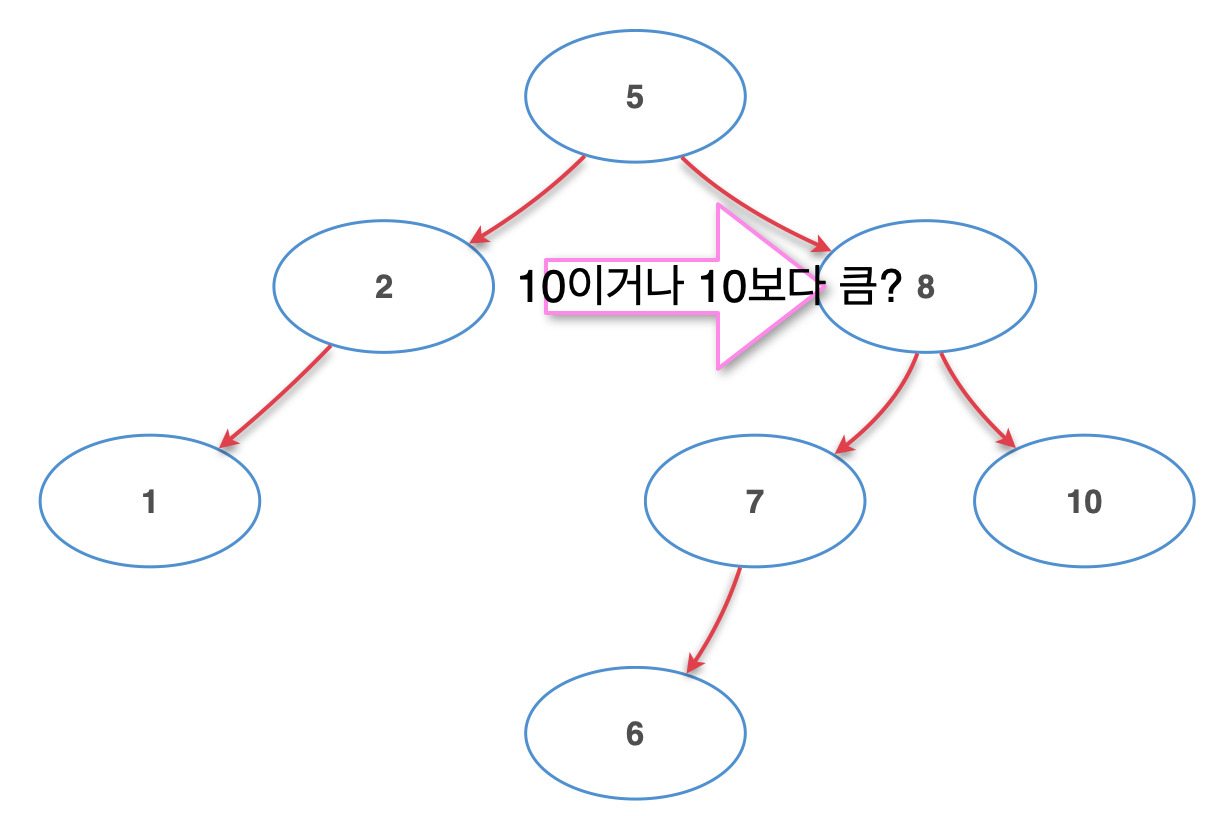
그 다음 노드인 8에게 10이거나 10보다 큰지를 물어본다. 10이라면 끝. 10이 아닌 경우 10보다 작다고 말할테니 오른쪽으로 이동.
3단계
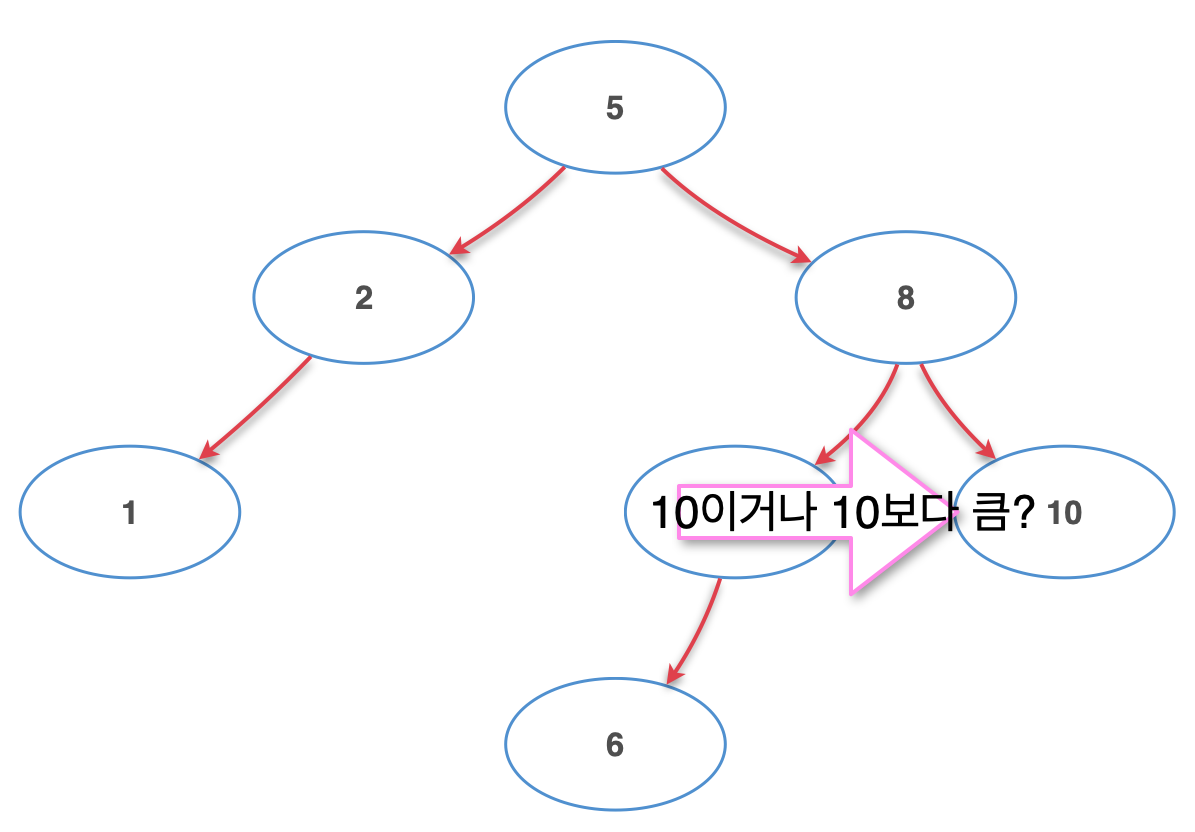
단 세번의 질문으로 원하는 10을 찾아냈다. 여기서 세번은 트리의 깊이(Depth)를 말한다.
5번 노드가 있는 1 Depth.
2, 8번 노드가 있는 2 Depth.
10번 노드가 있는 3 Depth.
이렇게 트리의 깊이만큼만 질문해서 원하는 답을 찾아낼 수 있다.
Binary Tree vs Binary Search Tree
Binary Search Tree
N개의 노드를 가진 꽉 찬 트리의 경우 트리의 깊이는 log N이다.
그래서 이 Binary Search Tree 구조로 원하는 값을 찾을 때 시간 복잡도는 O(log N)이다.
Binary Tree
정렬된 트리가 아니라 원하는 값을 찾기 위해 DFS 또는 BFS를 통해 찾아낸다.
결국 최악의 경우 N개의 노드를 가진 트리에서 N의 값을 찾는 시간 복잡도는 O(N)이다.
따라서 Binary Search Tree가 더 빠른 속도로 원하는 값을 찾아낼 수 있다.
Binary Search Tree 코드로 구현해보기
struct Node* find_node(struct Node* root, int findValue) {
if (root == NULL || root->value == findValue) {
return root;
} else if (root->value > findValue) {
return find_node(root->left, findValue);
} else {
return find_node(root->right, findValue);
}
}
위 코드가 Binary Search Tree 구조에서 원하는 값을 찾아내는 코드이다. 역시 Recursion(자기 자신 참조)을 통해 간단하게 구현할 수 있다. 순서대로 한 번 접근해보자.
1. 10을 찾고싶다고 할때, root node인 5가 최초로 들어온다.
2. root(5)는 NULL이 아니고 root(5)가 가진 값이 10이 아니므로 다음 if로 간다.
3. root(5)가 가진 값 5가 찾고자하는 값 10보다 크지 않기 때문에 다음 else로 간다.
4. 자기 자신을 호출한다 이때 파라미터는 root(5)의 오른쪽 노드 8과 찾고자하는 값 10.
5. 역시 root(8)는 NULL이 아니고 root(8)가 가진 값이 10이 아니므로 다음 if로 간다.
6. root(8)이 가진 값 8이 10보다 크지 않으므로 다음 else로 간다.
7. 자기 자신을 호출한다. 여기서 파라미터는 root(8)의 오른쪽 노드 10과 찾고자하는 값 10.
8. root(10)은 NULL이 아니지만, root(10)의 값 10과 찾고자 하는 값 10이 같으므로 이 root를 리턴한다.
9. 7번으로 돌아온다. 호출한 자기자신이 반환한 root(10)을 리턴한다.
10. 4번으로 돌아온다. 호출한 자기자신이 반환한 root(10)을 리턴한다. 끝.
이런식으로 절반을 소거해가면서 찾아내는 방법을 Binary Search라고 하고 그 구조가 Tree일 때 Binary Search Tree라고 한다.
Binary Search가 꼭 Tree여야하나?
그럼 여기서 질문이 생긴다. Binary Search는 꼭 트리일 필요는 없을 것 같다. 왜냐하면 배열에 값을 정렬해 놓아도 Binary Search로 검색할 수 있으니까. 맞다. 똑같이 시간 복잡도는 O(log N)이다.

이러한 정렬된 배열에 중간을 잡고 물어보면 똑같다.
1단계

정렬된 배열에 중간에 10이거나 10보다 큰지 물어본다. 10이라면 끝. 10이 아니면 10보다 작으니 오른쪽만 보면 된다.
2단계
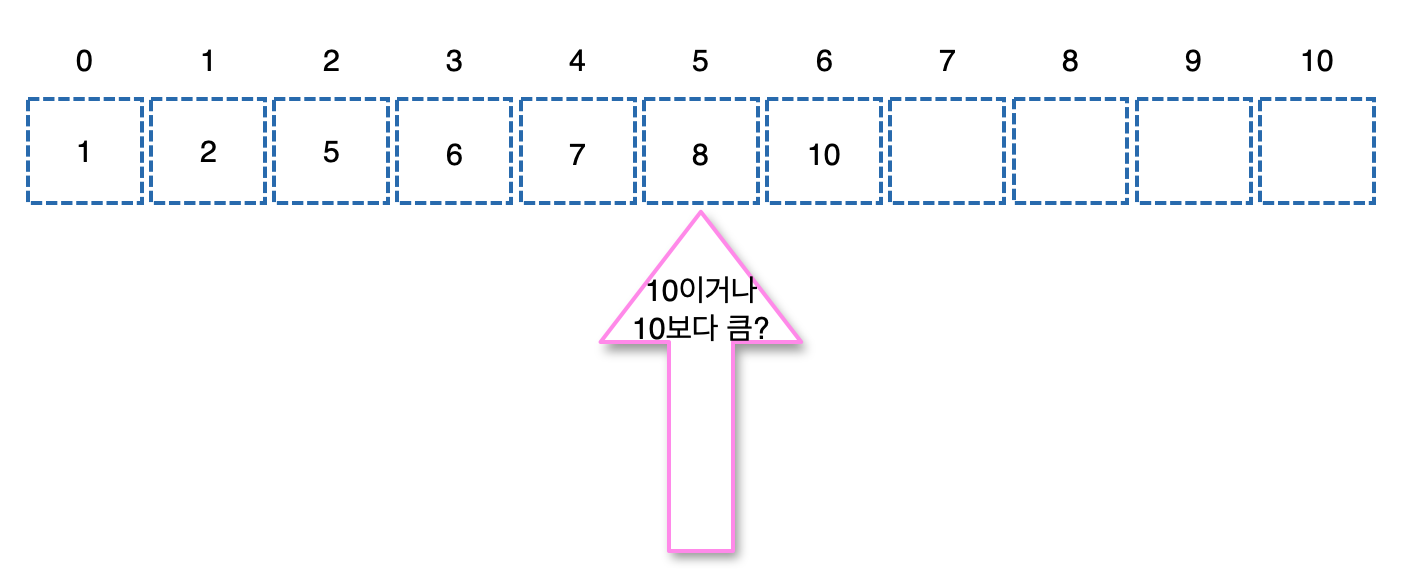
오른쪽을 기준으로 중간에서 10이거나 10보다 큰지 물어본다. 10이라면 끝. 10이 아니면 10보다 작으니 오른쪽만 보면 된다.
3단계

그럼 뭐하러 Binary Search Tree를 사용할까?
정렬된 배열에 값이 새로 추가되거나 제거되는 경우가 없으면 정렬된 배열이 더 좋을 수 있다.
근데, 새롭게 추가되는 값이 있을 땐 그 값을 추가한 후 다시 정렬을 해야하는 과정이 필요하다.
예를 들어보자, 저 배열에 4를 추가하고 싶다고 해보자.
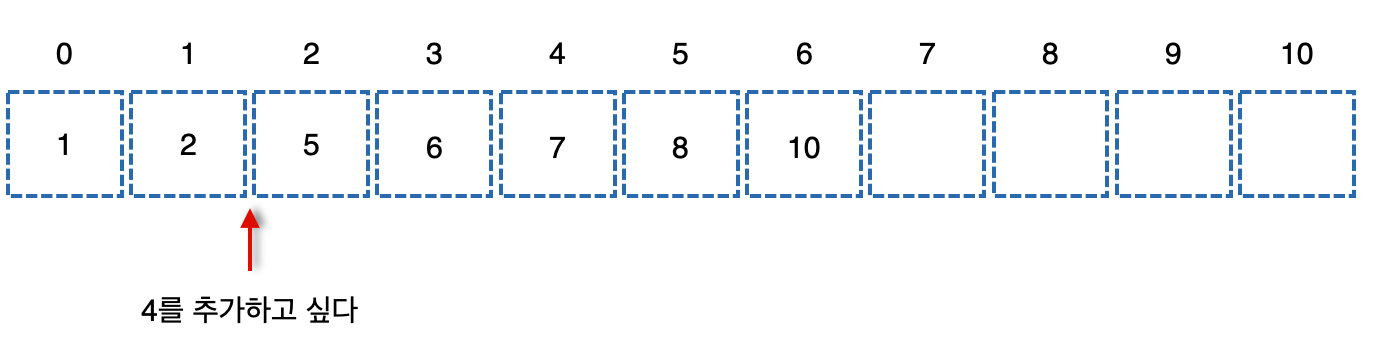
그럼 정렬을 위해 2와 5사이에 넣어야하고 그럼 5부터 마지막을 뒤로 전부 밀어야한다. 이 작업의 시간 복잡도는 O(N)이다.
근데! Binary Search Tree는 이 작업도 O(log N)이다.
"왜요?" Binary Search Tree에서 N개의 노드를 가진 꽉 찬 트리의 경우 깊이는 log N이라고 했고 그래서 트리에서 원하는 값을 찾을 때 질문의 횟수는 트리의 깊이(Depth)만큼이라고 했다.
그럼 원하는 자리를 찾는데 시간 복잡도는 O(log N).
원하는 자리를 찾았으니 추가하는(지우는) 시간 복잡도는 O(1).
두 경우를 모두 하는 시간 복잡도는 O(log N) + O(1) = O(log N)
O(N)과 O(log N)을 비교하면 압도적으로 빠른 수치다. 예를 들어, 전 세계 인구가 80억명이면 log(80억명) = 32이다.
80억개의 경우의 수를 Binary Search Tree로 만들면 내가 원하는 값을 찾는데 32번만에 가능하단 얘기다.
근데 O(N)은...? 최악의 경우.. 80억번..??
근데! 여기서 하나 더, 꽉 찬 트리가 아니면?
만약, Binary Tree는 Binary Tree인데 꽉 찬 트리가 아니라 이런 모양이면 어떻게 할까?

이것도 Binary Tree다. 자식이 최대 2개를 만족하고 오른쪽은 다 자신보다 크니까.
이런 경우 트리의 Depth만큼 찾아내는 시간 복잡도는 O(log N)이 아니라 O(N)이다.
결론부터 말하면 이런 경우는 고려하지 않아도 된다. Self-Balancing Binary Search Tree라는게 있는데 저런 모양이 나올 수 없게 새 노드가 추가되거나 삭제될 때 Binary Search Tree가 항상 Balance가 되도록 보장해준다.
Self-Balancing Binary Search Tree의 종류로 AVL Tree, Red Black Tree 이런게 있고 이런게 있다는 것 정도만 알아두자.
'자료구조' 카테고리의 다른 글
| 배열과 Big O 표기법 (0) | 2024.05.10 |
|---|---|
| Hash Table (2) | 2024.04.16 |
| Tree와 BFS / DFS (0) | 2024.04.16 |
| Stack (0) | 2024.04.15 |
| Queue (0) | 2024.04.15 |