참고자료:
김영한의 실전 자바 - 중급 2편 | 김영한 - 인프런
김영한 | 자바 제네릭과 컬렉션 프레임워크를 실무 중심으로 깊이있게 학습합니다. 자료 구조에 대한 기본기도 함께 학습합니다., 국내 개발 분야 누적 수강생 1위, 제대로 만든 김영한의 실전
www.inflearn.com
배열과 같이 여러 데이터(자료)를 구조화해서 다루는 것을 자료 구조라고 한다.
여러 형태의 자료 구조가 있지만 가장 기본이 되는 배열과 항상 이 자료구조하면 빼놓을 수 없는 Big O 표기법에 대해 다루고자 한다.
자바에서 배열을 선언할 땐 다음과 같이 선언한다.
package org.example.collection.array;
public class ArrayMain1 {
public static void main(String[] args) {
int[] arr = new int[5];
}
}
배열의 특징은 크기가 정해져있고, 정해진 크기만큼 연속적으로 메모리에 저장된다.
연속적으로 저장되기 때문에 가져가는 이점이 있다. 바로 배열에서 자료를 찾을 때 인덱스를 사용하면 매우 빠르게 자료를 찾을 수 있다. 구체적으로 단 한번의 계산으로 자료를 찾아낼 수 있다.
근데 어떻게 단 한번의 계산으로 가능한걸까? 항상 O(1)의 시간복잡도를 가진다. 이것만 알지 그 원리를 공부하고 있지 않았던거 같다.
만약, 위 코드처럼 타입이 int고 크기가 5인 배열을 생성하면 메모리에 이렇게 할당된다.
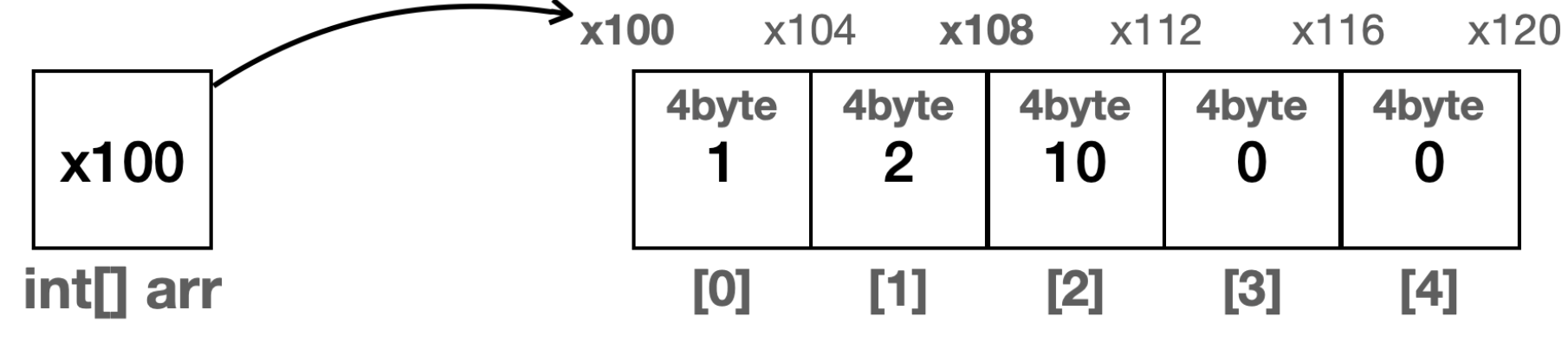
int는 4byte를 차지한다. 그래서 하나의 메모리 공간은 크기가 4byte이다.
그럼 배열의 시작 위치인 x100부터 시작해서 자료의 크기(4byte)와 인덱스 번호를 곱하면 원하는 메모리 위치를 찾을 수가 있는것이다.
arr[0] = x100 + (4byte * 0) = x100
arr[1] = x100 + (4byte * 1) = x104
arr[2] = x100 + (4byte * 2) = x108
이 연산이 배열이 왜 단 한번의 연산으로 조회가 가능한지를 설명한다. 아 그래서 배열은 크기와 타입을 정해주는구나?를 역으로도 생각할 수 있게 된다. 그래서 배열은 굉장히 좋은 자료구조 중 하나이다.
조회뿐 아니라 삽입, 삭제도 단 한번의 연산으로 가능하다.
- 삽입: arr[3] = 10
- 삭제: arr[3] = 0
딱 원하는 인덱스에 원하는 값을 추가하면 되고, 딱 원하는 인덱스를 찾아 값을 날리면 된다. 그래서 배열에서는 조회, 삽입, 삭제가 O(1)의 시간복잡도를 가진다. O(1)은 데이터가 아무리 많아도 1억개, 10억개, 1조개라도 단 한번의 연산이면 된다는 것을 의미한다.
근데 탐색은 O(n)이다. 왜냐하면 원하는 값을 찾기 위해선 처음부터 마지막까지 하나씩 순회를 해야만 내가 원하는 값을 찾아낼 수 있기 때문이다 배열의 크기가 N이면 연산도 N번만큼 필요하다.
물론, 저 위 그림을 예시로 배열에서 1을 찾고 싶다고 하면 0번 인덱스가 1이기 때문에 1번의 연산으로 찾는게 가능하지만 만약 30을 찾는다고 하면 0번 인덱스부터 4번 인덱스까지 갈 동안 찾지 못했기 때문에 배열의 크기만큼 연산이 이루어진다. 그리고 만약 마지막 인덱스에 원하는 값이 있어도 N번의 연산을 수행할것이다. 그래서 O(n)이 된다.
근데 여기서 말하는 O(1)이니 O(n), 이것들이 다 뭘까?
Big O 표기법
알고리즘의 성능을 분석할 때 사용하는 수학적 표현 방식이다. 처리해야 하는 데이터 양에 따라 그 알고리즘이 얼마나 빠르게 실행되는지 나타낸다. 정확한 실행 시간을 계산하는 게 아니고 데이터 양의 증가에 따른 성능의 변화 추세를 말한다.

- O(1) - 상수 시간을 말하고 데이터의 크기에 상관없이 일정하게 단 한번의 연산으로 처리된다.
- O(n) - 선형 시간을 말하고 입력 데이터의 크기에 비례하여 실행시간이 증가한다.
- O(n^2) - 제곱 시간을 말하고 알고리즘의 실행 시간이 입력 데이터의 크기의 제곱에 비례하여 증가한다. 예를 들면 이중 루프를 사용할 때이다.
- O(log n) - 로그 시간을 말하고 알고리즘의 실행 시간이 데이터 크기의 로그에 빌례하여 증가한다.
- O(n log n) - 선형 로그 시간을 말하고 대다수의 효율적인 정렬 알고리즘이 이렇다.
Big O 표기법은 데이터 양 증가에 따른 성능의 변화 추세를 비교하는데 사용한다. 쉽게 이야기해서 정확한 성능을 측정하는 것이 목표가 아니라 매우 큰 데이터가 들어왔을 때의 대략적인 추세를 비교하는 게 목적이다. 따라서 데이터가 매우 많이 들어오면 추세를 보는데 상수는 의미가 없어진다. 이런 이유로 Big O 표기법에서는 상수를 제거한다. 예를 들어 O(2n)이나 O(n+2), O(n/2) 모두 다 O(n)으로 표시한다.
Big O 표기법은 별도의 이야기가 없으면 보통 최악의 상황을 가정해서 표기한다. 최적, 평균, 최악의 경우로 나누어 표기하는 경우도 있다.
위 예시에서 배열을 가지고 얘기를 했는데 조회나 삽입, 삭제는 언제나 O(1)이다. 데이터가 아무리 많아도 단 한번의 수행으로 끝나니까.
탐색의 경우는 O(n)이다. 운이 좋으면 첫번째 인덱스가 원하는 값이 나올수도 있지만 최악의 경우는 가장 마지막 인덱스이거나 아예 없는 경우이기 때문에 N개의 요소를 다 확인한다.
'자료구조' 카테고리의 다른 글
| Hash Table (2) | 2024.04.16 |
|---|---|
| Binary Search Tree (0) | 2024.04.16 |
| Tree와 BFS / DFS (0) | 2024.04.16 |
| Stack (0) | 2024.04.15 |
| Queue (0) | 2024.04.15 |