Hash Table은 Key/Value Pair를 빠르게 저장하고 읽을 수 있는 자료구조이다.
파이썬에서 Dictionary라고 부르는 것이 이 Hash Table이다.
예를 들어, Key: Food, Value: Kimchi를 Hash Table에 저장하고자 하면 Hash Table한테 Key가 Food고 Value가 Kimchi인 이 Pair를 저장해 줘! 하고 저장을 한 다음 이후에 Food라는 Key의 Value가 어떻게 돼?라고 물어보면 Hash Table이 Kimchi입니다라고 말해주는 자료구조.
Hash Table의 구현 원리
이름 그대로 Table(배열)과 Hash Function으로 구성되어 있다.
Hash Function은 임의의 길이를 갖는 임의의 데이터를 고정된 길이의 데이터로 매핑하는 단방향 함수를 말한다.
쉽게 말하면 어떤 값이던간에 이 Hash Function에 넣으면 고정된 값(예를 들어 숫자)으로 만들어준다는 것을 말한다.
다음 그림을 보자.

어떤 값을 Input으로 만들던간에 Hash Function에 넣으면 위 조건처럼 10보다 작은 숫자 뱉어낸다.
중요한 건, Input이 같은 값이라면 Output도 무조건 같은 값으로 나온다.
그래서 Hash Table의 구성은 다음과 같다.
- Size가 N인 배열(Table)
- Output이 N보다 작은 Hash Function
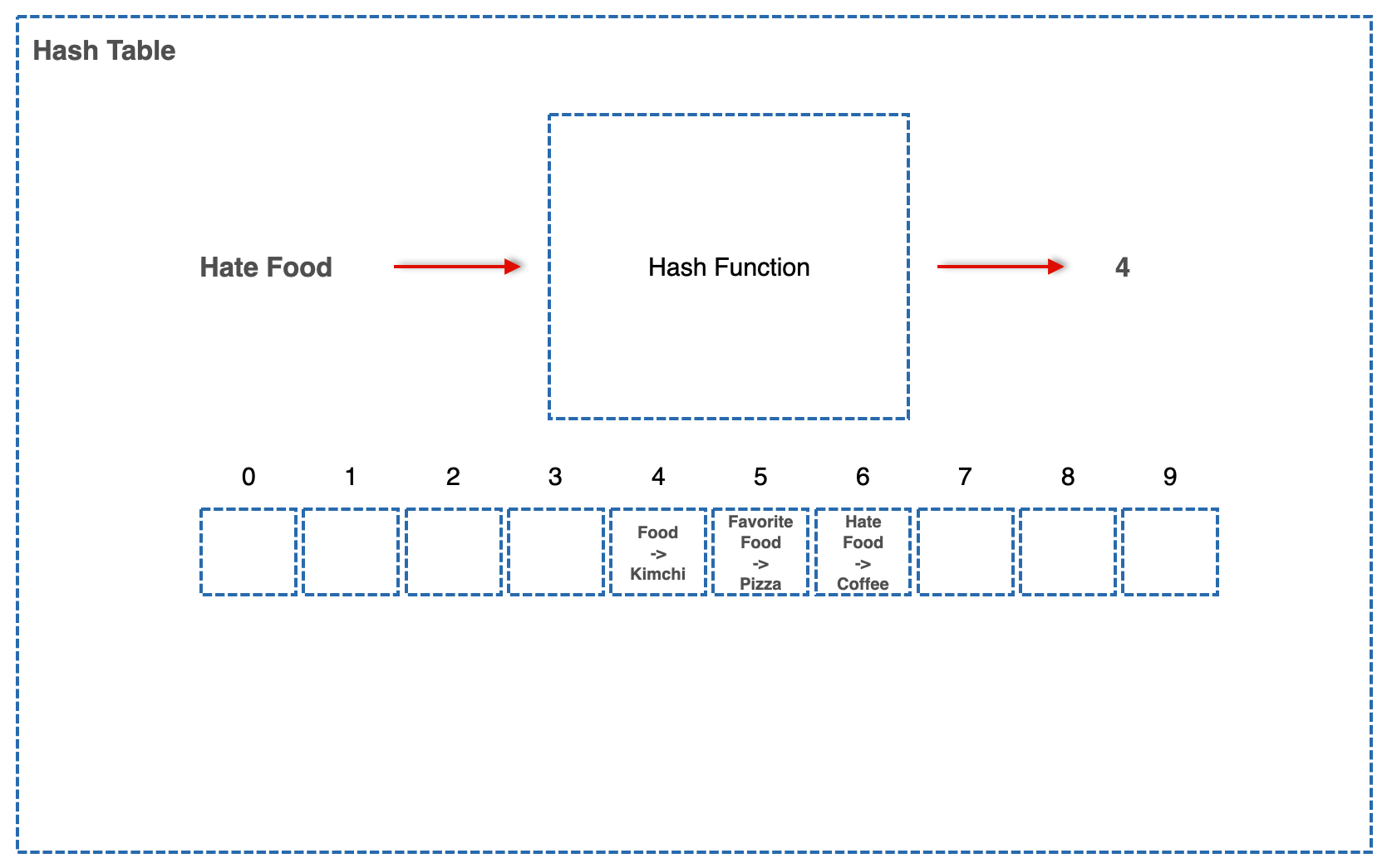
그래서 그림으로 보면 다음과 같다.
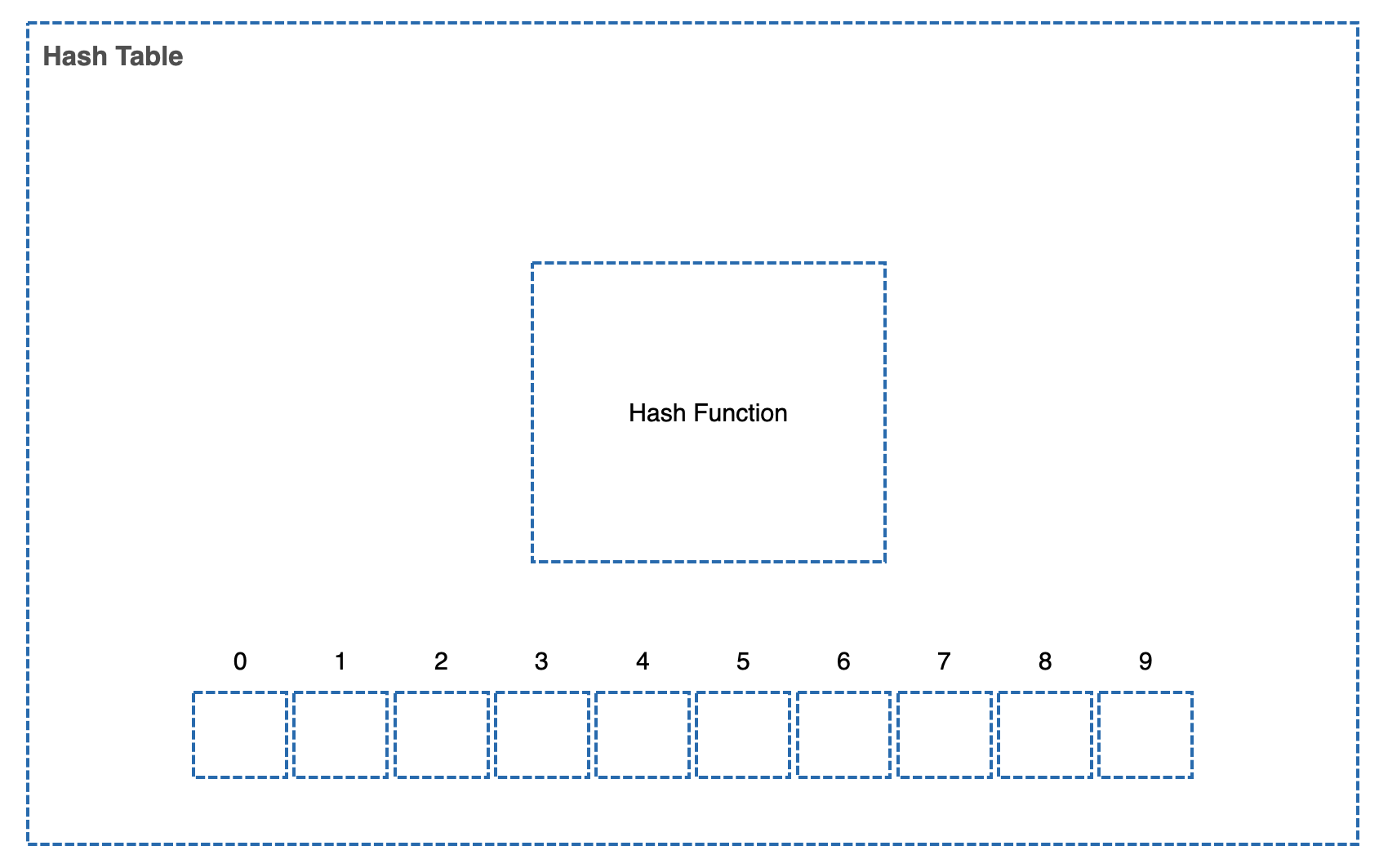
Hash Function, Table이 있는 Hash Table.
그래서 누군가가 Key "Food", Value "Kimchi"라는 Pair를 이 Hash Table에 저장하겠다고 한다.
1. Hash Table은 저 Key를 Hash Function에 집어넣는다. 그리고 나온 Output은 4.

2. 4라는 숫자를 가진 인덱스에 Value를 저장한다.
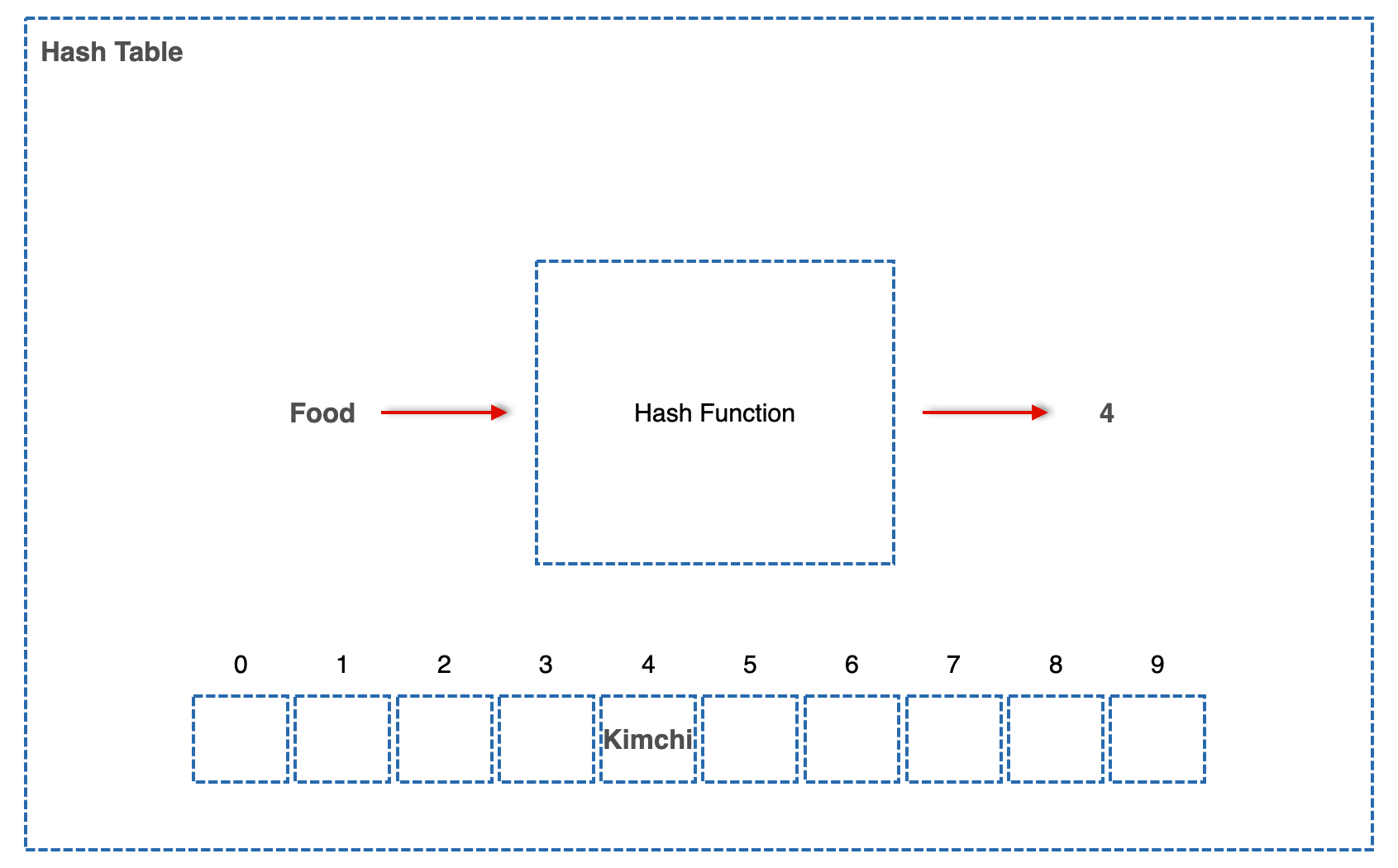
이게 아주 간단한 Hash Table인데 문제가 있다. 충돌의 문제.
예를 들어, 10개 이상의 값을 이 Hash Table에 넣으면 결국 Hash Function은 0 -10 사이의 숫자만을 뱉어내는 녀석이기 때문에 그 값들 중엔 중복되는 값이 생길 수밖에 없다.
간단한 예로, 위 그림처럼 인덱스 4에 Kimchi가 저장된 상태인데 누군가가 Key "FavoriteFood" Value "Pizza"라는 Pair를 이 Hash Table에 저장하려고 시도하는데 Hash Function이 같은 4를 뱉어냈다고 생각해 보면 아래 그림처럼 된다.
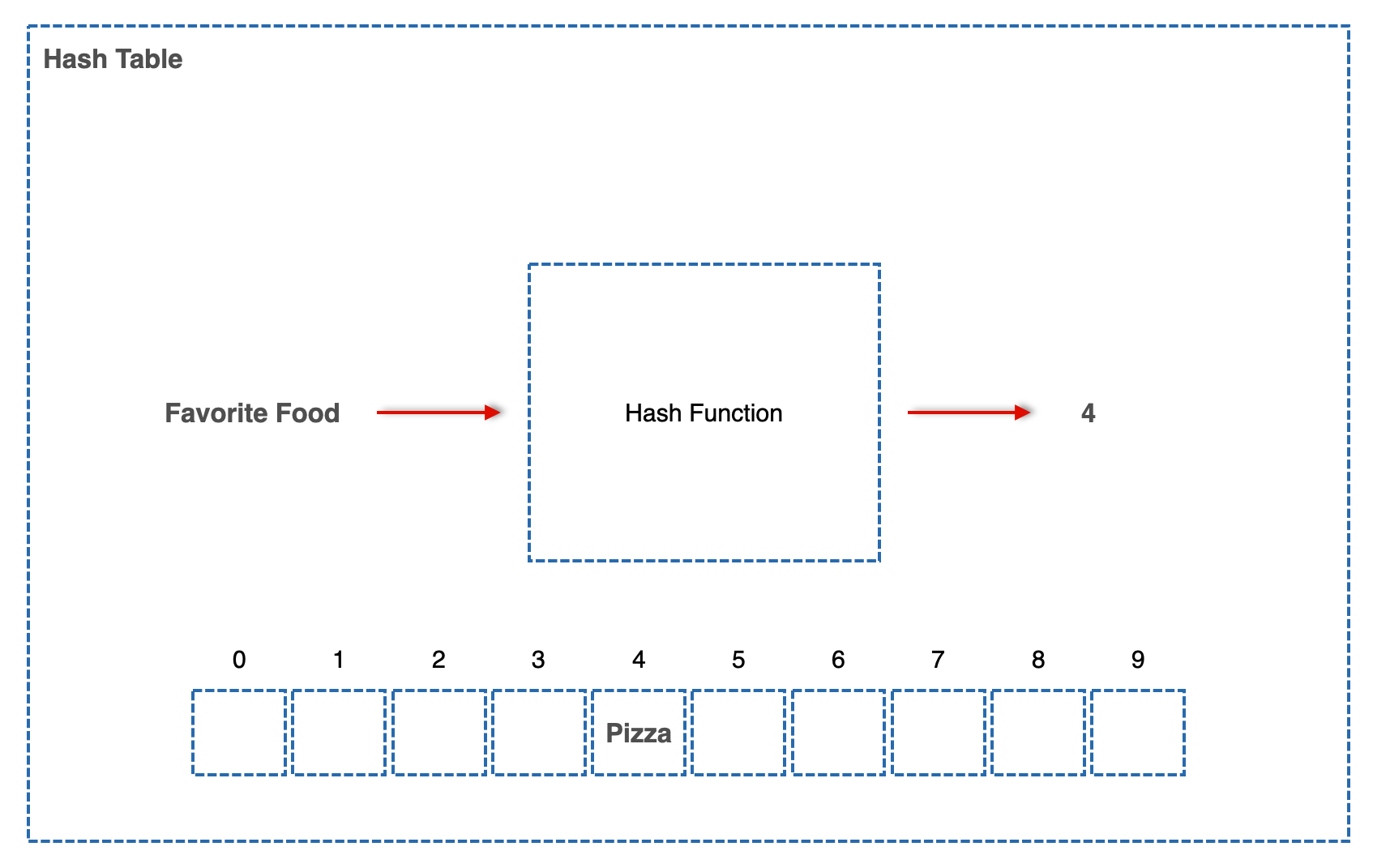
그럼 아까 Food/Kimchi를 저장했던 사람이 Food에 담긴 Value뭐야? 라고 물어보면 이 Hash Table은 Pizza라는 엉뚱한 값을 뱉을 수 있게 된다. 이걸 어떻게 해결할까?
Hash Table의 Collision 해결 방법
크게 두가지 방법이 있다.
- Chaining
- Probing
Chaining
우선 첫번째 방법인 Chaining은 그냥 배열을 쓰는 게 아니라 Linked List를 사용해서 Collision이 발생할 때마다 해당 인덱스(이 예시에선 4)에 있는 Linked List에 값을 연달아서 저장하는 것. 아래 그림을 보자.
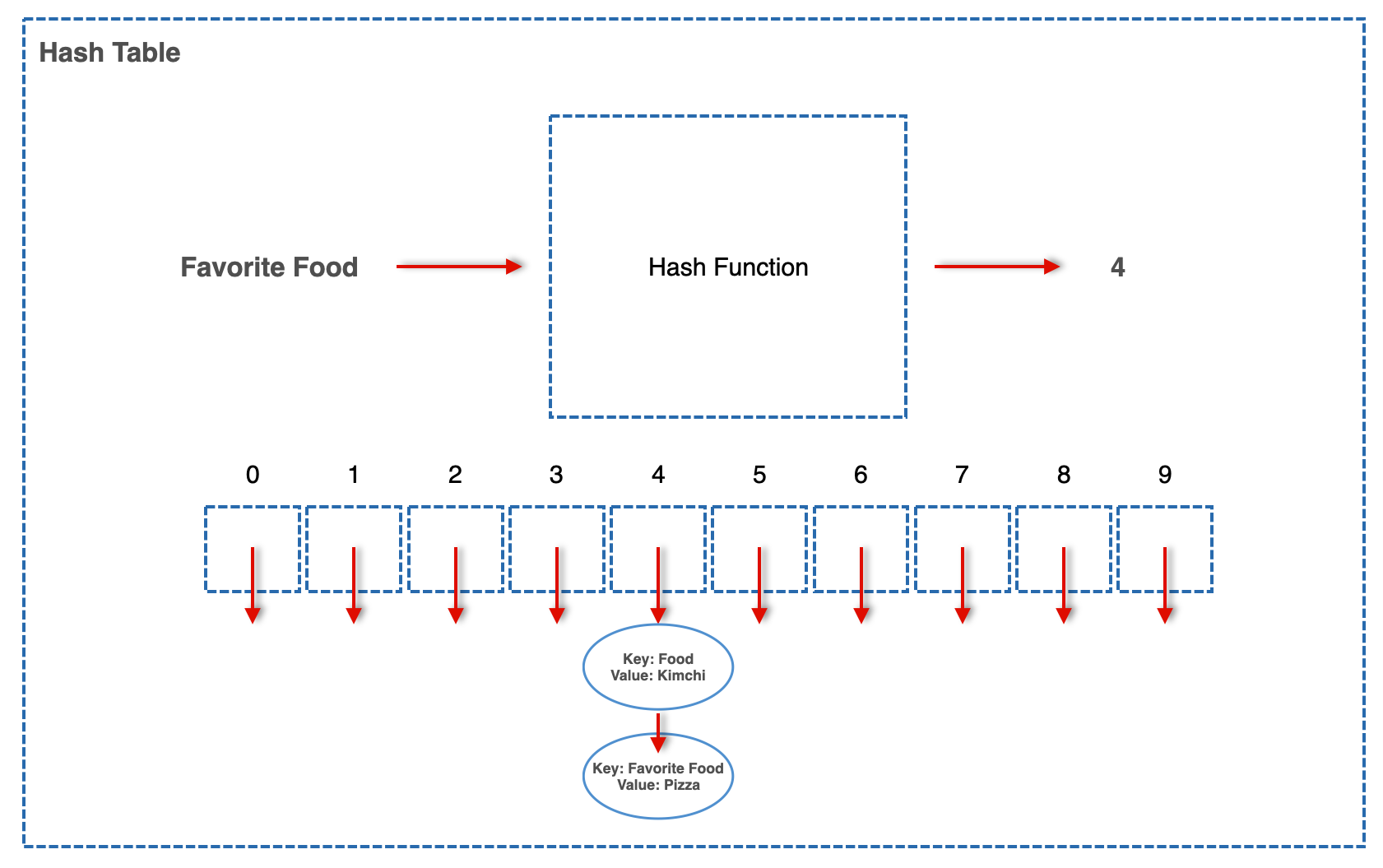
위 문제를 이런식으로 해결했다. 해당 인덱스에 Linked List로 차곡차곡 똑같이 넣는 것. 대신 이제는 Value만 넣을 순 없다. 이 Linked List에 여러 값이 들어가니까 어떤 Key에 해당하는지 알기 위해 Key/Value를 같이 넣어줘야 한다.
그래서 이제 유저가 "Key가 Food인 Value 찾아줘!" 하고 Hash Table에 요청을 하면 Hash Table은 먼저 Hash Function에 Input으로 Food를 넣어서 나온 값 4를 가진 메모리에 가면 나오는 Linked List에서 Iterator를 돌려서 원하는 값(Kimchi)을 찾아내는 것.
참고: Linked List 말고 Binary Search Tree를 사용해도 된다. 이전 포스팅에서 정리한 Binary Search Tree. 이 녀석을 사용하면 원하는 값을 찾아내는 시간 복잡도는 O(log N)이기 때문에 더 효율적일 수도 있다. 상황에 따라.
Probing
Probing도 여러 가지 방법이 있는데 그중 가장 간단한 Linear Probing을 보면 배열을 그대로 쓰고 Hash Function이 같은 값을 뽑아내면 우선 그 자리에 가보는데 값이 있을 때 그 옆을 보는 방식이다. 아래 그림을 보자.

1. Food/Kimchi라는 Pair를 Hash Table에 넣었더니 4번에 들어간 상태이다.
2. Favorite Food/Pizza라는 Pair를 Hash Table에 넣으려고 시도하는데 같은 4번이 나왔고 4번 자리를 보니 이미 값이 있어서 Hash Table이 그 옆자리에 넣었다.
이게 Linear Probing이다. 그래서 Linear Probing을 정리하자면,
- Linear Probing : 이미 자리에 값이 있으면 다음 자리에 추가한다.
근데, 이 문제의 단점이 있다. Collision이 많이 일어나면 그 주변에 병목현상이 생길 수 있다는 것.
예를 들어, 저 모양 그대로 HateFood/Coffee라는 Pair를 넣으려고 시도하는데 Hash Function이 또 4를 뱉어냈다. 그래서 4에 가보니 값이 있어서 그다음 5에 가보니 또 값이 있어서 6으로 가서야 넣게 됐다.
그래서 이 Linear Probing 문제를 또 해결하는 방법이 Quadratic Probing이다.
Quadratic Probing
다음 자리를 찾을 때 hash(x) + i가 아니라 hash(x) + i^2 자리에 넣는 방식이다. 그러니까 4가 나오면 Linear Probing은 5에 넣는 건데 Quadratic Probing은 16에 넣는다.
Hash Table의 시간 복잡도와 공간 복잡도
시간 복잡도
두 가지 케이스로 나뉠 수 있다.
- Hash Collision이 없을 때
- 데이터 추가
- Key 값 해시하기 O(1)
- 데이터 넣기 O(1)
- O(1) + O(1) = O(1)
- 데이터 읽기
- Key 값 해시하기 O(1)
- 데이터 읽기 O(1)
- O(1) + O(1) = O(1)
- 데이터 추가
- Hash Collision이 있을 때
- 데이터 추가/읽기
- Key 값 해시하기 O(1)
- 최악의 경우 데이터 넣기, 읽기가 O(N)이 될 수 있음.
- (왜냐하면, Hash Function이 잘못 만들어진 경우 계속해서 같은 Output을 만들어 내는 최악의 Hash Function이 있으면 Linked List 추가의 경우 마지막 자리를 알기 위해 1-N까지 데이터가 있을 때 처음부터 하나씩 자리를 찾아야 하고, 읽기의 경우 해당 데이터가 어디 있는지 알기 위해 N개의 노드를 다 뒤져야 할 수도 있으므로)
- 근데, 이건 정말 최악의 경우인 거고 어지간하면 O(1)이 된다. 우선 Key 값 해시하는 건 언제나 O(1)이고 Hash Function이 문제없이 잘 만들어졌다면 바로바로 데이터를 넣거나 읽을 수 있게 된다.
- 그래서 어지간하면 이 경우도 O(1)이 맞고, 정말 정말 잘못 만들어진 Hash Function이라면 O(N)이 될 수도 있다는 것으로 알아두면 좋을듯하다.
- 데이터 추가/읽기
공간 복잡도
구분 없이 O(N).
N개의 데이터를 넣으려면 그에 맞는 배열 사이즈가 있어야 하고(N) 해당 데이터 타입의 Byte를 가지는 메모리 공간(X) = N * X => O(N).
'자료구조' 카테고리의 다른 글
| 배열과 Big O 표기법 (0) | 2024.05.10 |
|---|---|
| Binary Search Tree (0) | 2024.04.16 |
| Tree와 BFS / DFS (0) | 2024.04.16 |
| Stack (0) | 2024.04.15 |
| Queue (0) | 2024.04.15 |